ชุดการแยกตัวประกอบ (ชุดผลบวกของกำลังสาม) [Factorisation (Sum of Cubes)]

Description

วิธีการเล่น

สื่อการเรียนรู้ชุดนี้จะใช้การนำตัวเล่นทรงสี่เหลี่ยมมุมฉากประกอบเป็นทรงลูกบาศก์ พิจารณาความสัมพันธ์ของปริมาตรของทรงลูกบาศก์ที่ได้ จากนั้นแยกตัวเล่นทรงสี่เหลี่ยมมุมฉากออกเป็น 3 ส่วน แล้วพิจารณาความสัมพันธ์ของปริมาตรของตัวเล่นไม้ทรงสี่เหลี่ยมมุมฉากแต่ละส่วน เชื่อมโยงสู่

การแยกตัวประกอบผลบวกของกำลังสาม

ตัวอย่างเช่น

1. พิจารณาสื่อการเรียนรู้ หากต้องการแยกตัวประกอบผลบวกของกำลังสาม

ทำได้โดยกำหนดให้

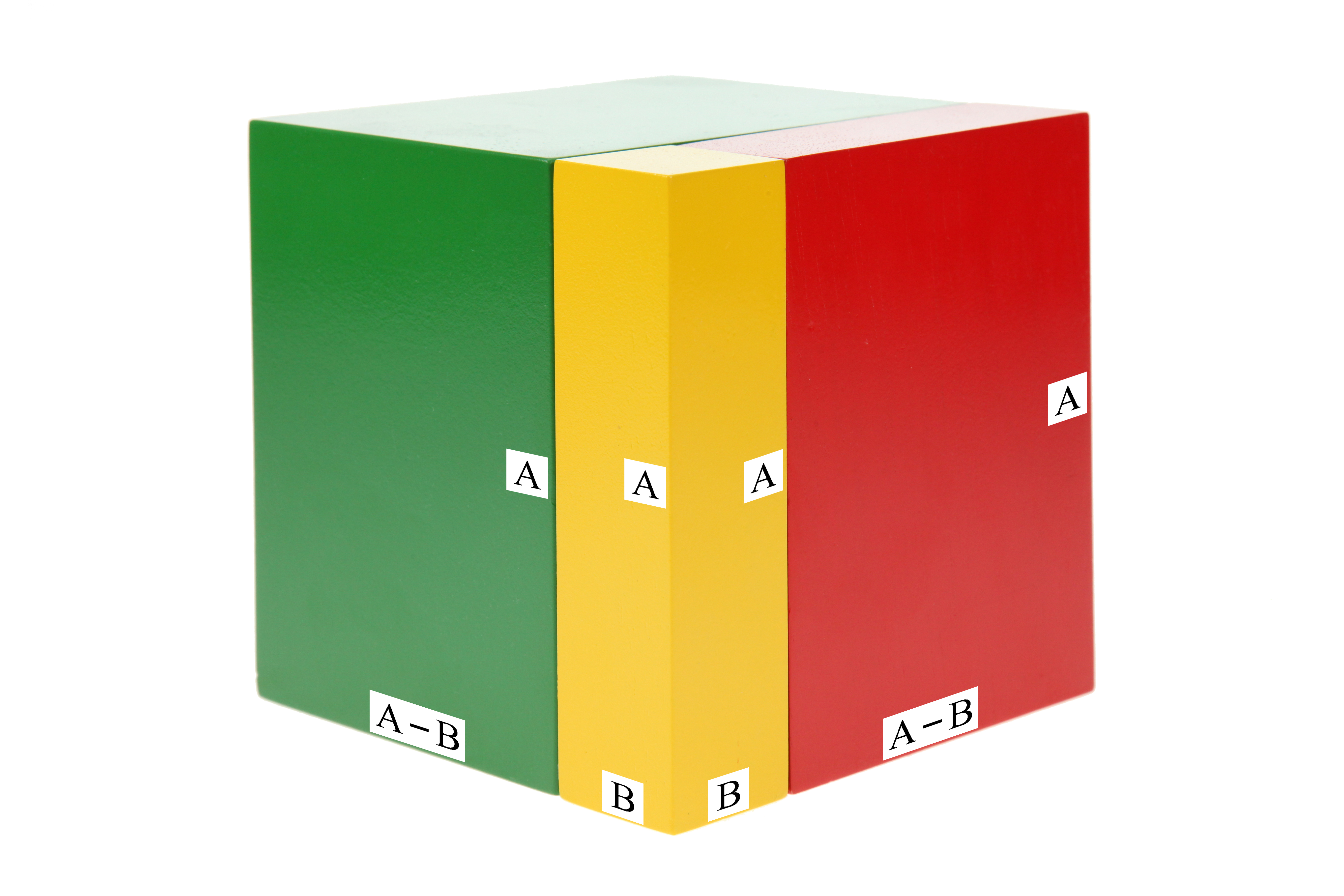
ตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเขียว          มีความกว้าง A – B หน่วย มีความยาว A หน่วย

และมีความสูง A หน่วย

ตัวเล่นทรงสี่เหลี่ยมมุมฉากสีแดง          มีความกว้าง B หน่วย มีความยาว A – B หน่วย

และมีความสูง A หน่วย

ตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเหลือง       มีความกว้าง B หน่วย มีความยาว B หน่วย

และมีความสูง A หน่วย

ตัวเล่นทรงสี่เหลี่ยมมุมฉากสีน้ำเงิน       มีความยาวแต่ละด้านยาว B หน่วย

(อาจใช้ป้ายสติกเกอร์ เขียน A B และ A – B แล้วติดกำกับไว้ในแต่ละตัวเล่น)

2. ปริมาตรของตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเขียว = ความกว้าง x ความยาว x ความสูง

=   A²(A – B)              ลูกบาศก์หน่วย

ปริมาตรของตัวเล่นทรงสี่เหลี่ยมมุมฉากสีแดง       =   ความกว้าง x ความยาว x ความสูง

=   AB(A – B)             ลูกบาศก์หน่วย

ปริมาตรของตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเหลือง    =   ความกว้าง x ความยาว x ความสูง

=   B²A                      ลูกบาศก์หน่วย

ปริมาตรของตัวเล่นทรงสี่เหลี่ยมมุมฉากสีน้ำเงิน     =   (ความยาวแต่ละด้าน)³

=   B³                                    ลูกบาศก์หน่วย

3. นำตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเขียว สีแดง และสีเหลืองมาประกอบกัน ซึ่งจะได้ทรงสี่เหลี่ยมมุมฉากรูปใหญ่ โดยทรงสี่เหลี่ยมมุมฉากรูปใหญ่ มีความยาวแต่ละด้านยาว A หน่วย

ปริมาตรของทรงสี่เหลี่ยมมุมฉากรูปใหญ่           =    (ความยาวแต่ละด้าน)³

=    A³                     ลูกบาศก์หน่วย

4. นำตัวเล่นทรงสี่เหลี่ยมมุมฉากสีน้ำเงินมาประกอบเข้ากับทรงสี่เหลี่ยมมุมฉากรูปใหญ่ โดยวางไว้บนตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเหลือง พบว่า

ปริมาตรของทรงสี่เหลี่ยมมุมฉากทั้งหมด                =    ปริมาตรของทรงสี่เหลี่ยมมุมฉากรูปใหญ่

+ ปริมาตรของทรงสี่เหลี่ยมมุมฉากรูปเล็ก

=    A³ + B³             ลูกบาศก์หน่วย

5. แยกตัวเล่นทรงสี่เหลี่ยมมุมฉากทั้งหมดที่ประกอบกันไว้ ออกมาพิจารณาเป็น 3 ส่วน คือ

ส่วนที่ 1 เป็นตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเขียว ส่วนที่ 2 เป็นตัวเล่นทรงสี่เหลี่ยมมุมฉากสีแดง และ

ส่วนที่ 3 เป็นตัวเล่นทรงสี่เหลี่ยมมุมฉากสีเหลืองรวมกับสีน้ำเงิน (ซึ่งมีความกว้าง B หน่วย มีความยาว

B หน่วย และมีความสูง A + B หน่วย โดยมีปริมาตร = B²(A + B) ลูกบาศก์หน่วย) แล้วพิจารณา

หาความสัมพันธ์

6. จากสื่อการเรียนรู้ สามารถพิจารณาความสัมพันธ์ได้ คือ

ปริมาตรของทรงสี่เหลี่ยมมุมฉากทั้งหมด

= ปริมาตรของส่วนที่ 1 + ปริมาตรของส่วนที่ 2 + ปริมาตรของส่วนที่ 3

A³ + B³  = A²(A – B) + AB(A – B) + B²(A + B)

= (A – B)(A² + AB) + B²(A + B)

= (A – B)A(A + B) + B²(A + B)

= A(A – B)(A + B) + B²(A + B)

= (A + B){A(A – B) + B²}

= (A + B)(A² – AB + B²)

7. สรุปได้ว่า A³ + B³ = (A + B)(A² – AB + B²)

 

ข้อแนะนำสำหรับผู้ปกครอง

ผู้ปกครองควรแนะนำให้นักเรียนปฏิบัติกิจกรรมด้วยตนเอง เพื่อนักเรียนจะได้สร้างองค์ความรู้

เป็นของตนเองและในระหว่างการปฏิบัติกิจกรรมควรตั้งคำถามกระตุ้นความคิดในแต่ละขั้นตอน

จากนั้นให้นักเรียนนำเสนอหลักการแยกตัวประกอบผลบวกของกำลังสาม พร้อมสรุปองค์ความรู้ที่ได้

จากการสังเกต โดยมีผู้ปกครองคอยตรวจสอบความถูกต้อง